Inhaltsverzeichnis
Zusammenfassung
Faserverstärkte Kunststoffe können aus einem Zusammenschluss einzelner Schichten zu einem Mehrschichtverbund bestehen. Bei unidirektionalen Schichten ergeben sich je nach Belastungsfall und Orientierung der Schichten unterschiedliche Beanspruchungsprofile dessen. Mit welcher Orientierung jede einzelne Schicht gelegt werden sollte um eine optimale Auslastung des Mehrschichtverbunds zu erreichen, ist die hier behandelte Problemstellung. Dies ist ein Optimierungsproblem, für das hier eine Systematik zur Lösung entwickelt wird. Dafür wird sich zunächst ein Überblick über ähnliche Studien in der Literatur verschafft wo unterschiedliche naturinspirierte Optimierungsverfahren eingesetzt wurden. Sodann wird die Evolutionsstrategie ausgewählt und diese auf die vorliegene Problemstellung angewandt. Es werden Parameterstudien durchgeführt um Korrelationen hinsichtlich der Leistungsfähigkeit und Ergebnisgüte zu ermitteln. Diese dienen dann als Grundlage zur Untersuchung von zugrundeliegenden Gesetzmäßigkeiten.
Einleitung
Faserverstärkte Kunststoffe (FVK) sind heute moderne Werkstoffe, die in einer Vielzahl von Produkten und ihren Komponenten ihre Anwendung finden. Nachdem das Potential von Stählen und andere Metalllegierungen allmählich ausgereizt ist, werden große Hoffnungen in diese noch relativ junge Technologie gesetzt. Hervorragende gewichtsspezifische Eigenschaften wie beispielsweise Festigkeit und Steifigkeit prädestinieren sie dafür, signifikante Gewichtseinsparungen möglich werden zu lassen. Gleichzeitig sind FVK aber auch in vielerlei Hinsicht sensibler und erhalten ihre Tragfähigkeit durch vollkommen andere Prinzipien als Metalle. Dadurch ergeben sich Chancen wie auch Herausforderungen. Der größte Unterschied besteht darin, dass Lasten im Grunde nur durch die Fasern aufgenommen werden können; der sie umgebende Kunststoff ist im Verhältnis dazu schwach und hat andere Aufgaben.
Am deutlichsten wird das bei den sogenannten unidirektional verstärkten Gelegen, kurz: UD-Gelegen. Dies sind dünne Flächengebilde, genannt Laminae oder Einzelschichten, deren Endlosfasern nur in einer Richtung liegen und dadurch auch nur monodirektional nennenswerte Lasten aufnehmen können. Solche Schichten werden übereinander angeordnet und als Mehrschichtverbund (folgend auch „Laminat“ genannt) eingesetzt. Angesichts der Belastung, der Randbedingungen und allen anderen Auslegungsparametern die je nach Anwendungsfall höchst unterschiedlich sein können, stellt sich nun die Frage, in welchen Orientierungen die Schichten anzuordnen sind um das beanspruchungsgerechte Eigenschaftsprofil zu erhalten – ein Optimierungsproblem.
Deterministische Optimierungsverfahren wie beispielsweise der Simplex-Algorithmus konvergieren mitunter (zu) früh zu einem lokalen Optimum. Um möglichst nah an das tatsächliche Optimum zu kommen ist ein vielversprechender Ansatz hingegen, naturinspirierte, heuristische Optimierungsverfahren zu verwenden. Sie können auch bei einer hohen Anzahl von Parametern und schwierigen Zielfunktionen (zum Beispiel nicht-konvex, unstetig usw.) mit hoher Wahrscheinlichkeit optimale Lösungen ermitteln. Entscheidend dafür ist allerdings, wie man die Eingabeparameter des Algorithmus wählt damit er leistungsfähig, d.h. effizient und zuverlässig diese Ergebnisse liefert.
Die Auswahl eines geeigneten Optimierungsalgorithmus, die Anwendung auf Laminate mit unterschiedlicher Anzahl an Einzelschichten, die Handhabung der Eingabeparameter und die Auswertung der Ergebnisse sind Gegenstand dieser Arbeit.
Klassische Laminattheorie
Das Laminatmodell besteht aus einer beliebig wählbaren Anzahl von übereinander angeordneten unidirektionalen Gelegen, im hier vorliegenden Fall Schichten aus glasfaserverstärktem Kunststoff (GFK). Die hier verwendeten Kennwerte sind in Tabelle 1 aufgelistet. Für die Einzelschichten wird jeweils von einem ebenen Spannungszustand ausgegangen, was bedeutet, dass Spannungen in Richtung der Dicke je Schicht vernachlässigt werden, sie also als Scheiben/Platten mit in der Ebene auftretenden Beanspruchungen betrachtet werden. Es gilt also σz=τzx=τyz=0. Die Grundbeanspruchungen sind demnach Zug in Faserrichtung, Zug quer zur Faserrichtung und Schub in der Flächenebene. Einflüsse aus der Fertigung wie etwa Klebung, materielle Inhomogenitäten oder differierende Fasergehalte werden vernachlässigt. Es handelt sich also um ein idealisiertes Modell.
Hier wird die Scheiben-/Plattentheorie nach Kirchhoff-Love abgebildet. Im Hinblick auf die klassische Laminattheorie beschreibt sie folgende Annahmen:
- Die Plattendicke ist klein im Vergleich zu den übrigen geometrischen Ausdehnungen
- Die Durchbiegung der Platte ist klein im Vergleich zur Dicke und die Neigungen sind klein im Vergleich zu Eins.
- Gerade Linienabschnitte, die ursprünglich orthogonal auf der Mittelfläche standen, sind auch im verformten Zustand gerade und orthogonal zur verformten Mittelfläche (Verzerrungen sind linear über die Plattendicke verteilt).
- Die Spannungen σz normal zur Mittelfläche (MF) dürfen vernachlässigt werden
- Zwischen den Einzellagen besteht vollkommene Haftung (idealisierter Verbund)
| E1 (MPa) | E2 (MPa) | ν12 | ν21 | G12 (MPa) | Dicke (mm) |
|---|---|---|---|---|---|
| 44500 | 12500 | 0,28 | ν12 ∙ E2/E1 | 6000 | 0,2 |
Die Berechnungen der Spannungen jeder einzelnen Schicht, die sich aus der Laminatbelastung ableiten kann in folgenden Schritten zusammengefasst werden:
Zunächst werden die vier unabhängigen Materialkennwerte jeder Schicht, die sich aus ihren transversalisotropen mechanischen Eigenschaften ergeben ermittelt, indem man mikromechanische Modelle anwendet, Versuche durchführt oder sie der Literatur entnimmt. Hiermit kann nun je Schicht die sogenannt „lokale“ Steifigkeitsmatrix aufgestellt werden, in der die 1-Richtung die Faserrichtung kennzeichnet und die 2-Richtung jene senkrecht zur Faserrichtung. Die Steifigkeitsmatrix lautet damit:
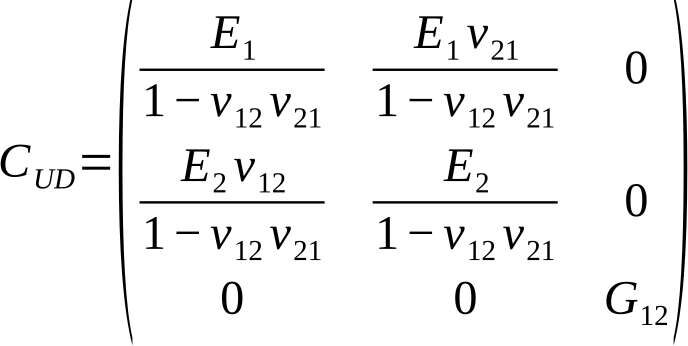
Die Dehnungs-Steifigkeitsbeziehung entsprechend HOOKEschem Stoffgesetzt ergibt sich mit σUD=CUD ∙ εUD zu:
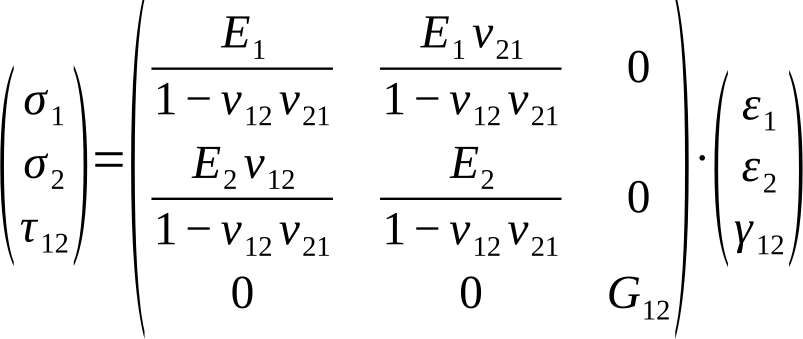
Die Steifigkeitsbeziehungen für jede Schicht sind hiermit bezüglich ihrer lokalen Koordinatensysteme beschrieben. Der nächste Schritt besteht darin, sie in ein globales Koordinatensystem des Verbunds zu überführen. Dies geschieht mittels der Transformationsmatrix TФ:
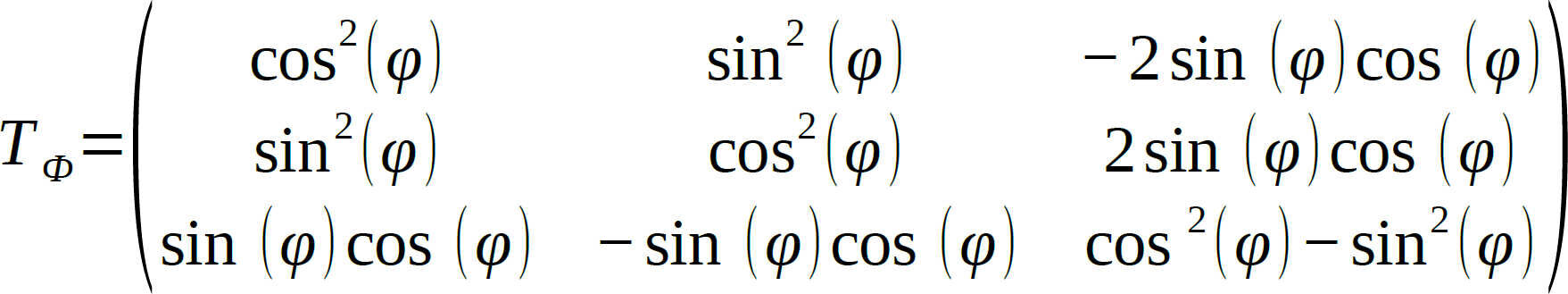
Die Überführung wird beschrieben durch
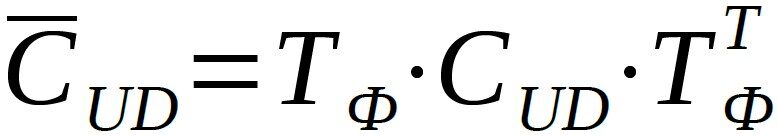
Damit ist die Beschreibung der Spannungs-Dehnungsbeziehung der Schichten sowie deren Drehung in ein gemeinsames, globales Koordinatensystem vollzogen. Anschließend wird mittels der statischen Gleichgewichtsbedingungen die sogenannte ABD-Matrix aufgestellt, die die Zusammenhänge von Schnittgrößen (Kraft- und Momentenflüsse) mit den Dehnungen und Wölbungen des Laminats ausdrückt. Der Name stammt aus dem Umstand heraus, dass diese Matrix zu viermal je 3×3-Matrizen besteht, und zwar aus einmal einer A-Matrix, die die Eigenschaften der Scheibe darstellt, einmal einer D-Matrix die die Eigenschaften der Platte repräsentiert und zweimal einer B-Matrix, die die Kopplung von Schnittkräften und –momenten bzw. Dehnungen und Wölbungen beschreibt. Mit N für die Schnittkräfte, M für die Schnittmomente, ε für die Dehnungen und κ für die Wölbungen ergibt sich diese Beziehung zu:
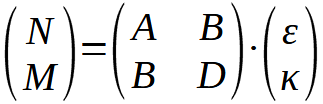
Mit der Ermittlung der Schnittkräfte aus dem statischen Gleichgewicht können nun die globalen Dehnungen und sodann die globalen Spannungen ausgerechnet werden. Diese werden nun wieder rücktransformiert um die vorherrschenden Beanspruchungen im jeweiligen Schichtkoordinatensystem zu bestimmen. Hiernach können sodann Versagenskriterien zur Anwendung kommen um die Festigkeit eines Laminats zu bewerten und seine Zulässigkeit zu bestimmen. Für Details zur klassischen Laminattheorie und deren Herleitung siehe [1].
Versagenskriterium nach CUNTZE
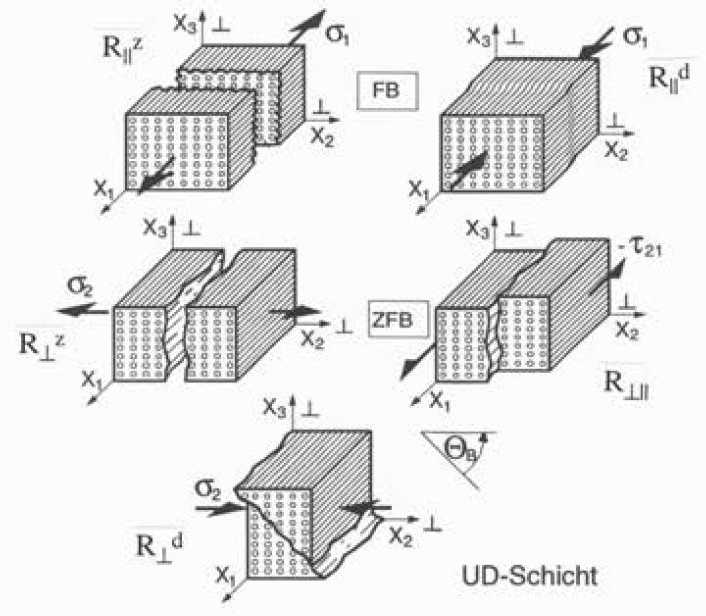
Das Versagenskriterium nach CUNTZE (für Details hierzu siehe [2]) mit seinem beschriebenen Failure Mode Concept wird in dieser Arbeit zur Anwendung kommen. Es unterscheidet das Versagen durch fünf unterschiedliche Bruchmoden, und zwar:
- Faserbruch („FB“ bzw. „FF“ für Fiber Failure) bei
- Zugbeanspruchung längs zur Faser R||z
- Druckbeanspruchung längs zur Faser R||d
- Zwischenfaserbruch („ZFB“ bzw. „IFF“ für Inter-Fiber-Failure) bei
- Zugbeanspruchung quer zur Faserrichtung R⊥z
- Druckbeanspruchung quer zur Faserrichtung R⊥d
- Scherbeanspruchung längs zur Faserrichtung R⊥||
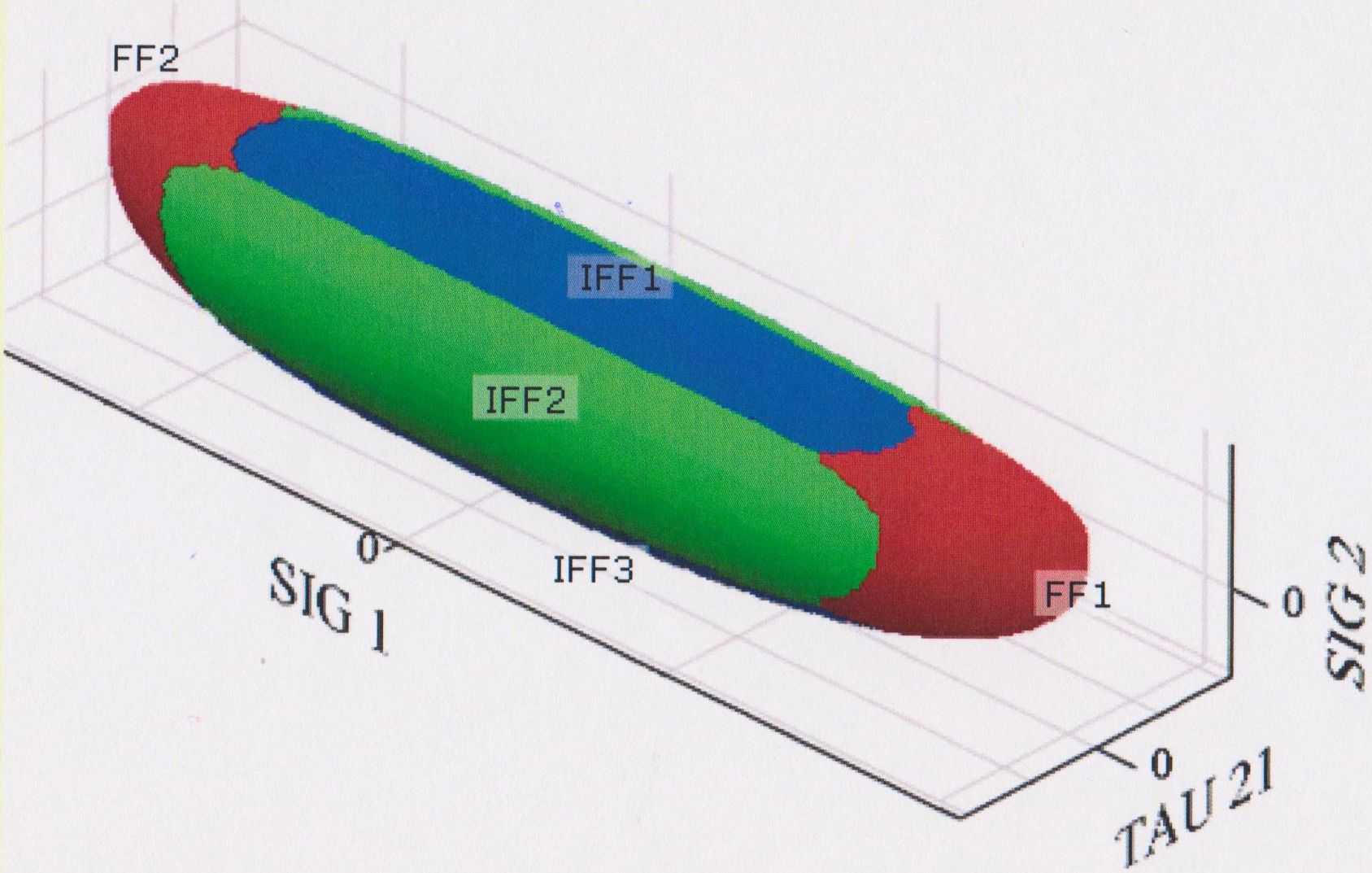
Es gibt grundsätzlich zwei verschiedene Ansätze zu definieren wann Versagen eintritt, und zwar das Erstschichtversagen („first-ply-failure“) sowie das Letztschichtversagen („progressive-failure“). Beim Erstschichtversagen tritt der Versagensmoment ein, wenn eine Schicht des Laminats ihre Tragfähigkeit verliert. Das Laminat bleibt sodann mit einer Restfestigkeit bzw. –steifigkeit zurück. Beim Letztschichtversagen findet Versagen statt, wenn auch die letzte Einzelschicht ihre Tragfähigkeit verloren hat. Hier findet der Ansatz des Erstschichtversagens Anwendung.
Naturinspirierte Optimierung von Composites: Stand heute
Zunächst wird sich ein Überblick darüber verschafft, wie faserverstärkte Kunststoffe mittels naturanaloger Verfahren optimiert werden. Hierbei ist insbesondere von Interesse, mit welcher Häufigkeit welche Algorithmen eingesetzt wurden. Die Frage die sich also stellt ist, ob sich ein Muster hinter der Häufigkeit des spezifischen Optimierungsziels und der hierfür verwendeten Algorithmen erkennen läßt. Darüber hinaus wird geprüft, ob sich hiervon Rückschlüsse auf die These ableiten lassen, dass es für jedes Optimierungsziel das man auf FVK anwendet den passenden Algorithmus gibt.
Die Datenbanken bzw. Suchmaschinen in denen die Recherche nach wissenschaftlichen Veröffentlichungen im Internet getätigt wird, sind www.Scopus.com und www.ScienceDirect.com. Diese werden nach der Anwendung folgender Optimierungsalgorithmen durchsucht:
- Genetischer Algorithmus (GA)
- Evolutionsstrategie (ES)
- Particle Swarm Optimization (PSO)
- Ant Colony Optimization (ACO)
- Artificial Bee Colony (ABC)
- Artificial Immune System (AIS)
Durch Kombination von Schlagwörtern wie „laminate, CFRP, lay-up, stacking sequence, composite, fiber reinforced, optimization, evolutionary optimization, evolutionary algorithm, nature-inspired, bio-inspired, ant colony, particle swarm” usw. werden die Veröffentlichungen gesucht und gesammelt. Anschließend folgt die Sortierung der Veröffentlichungen, und zwar zunächst nach ihrem Optimierungsziel und anschließend nach dem verwendeten Algorithmus. Die Mehrzieloptimierung wird separat, jedoch nach gleichem Muster behandelt.
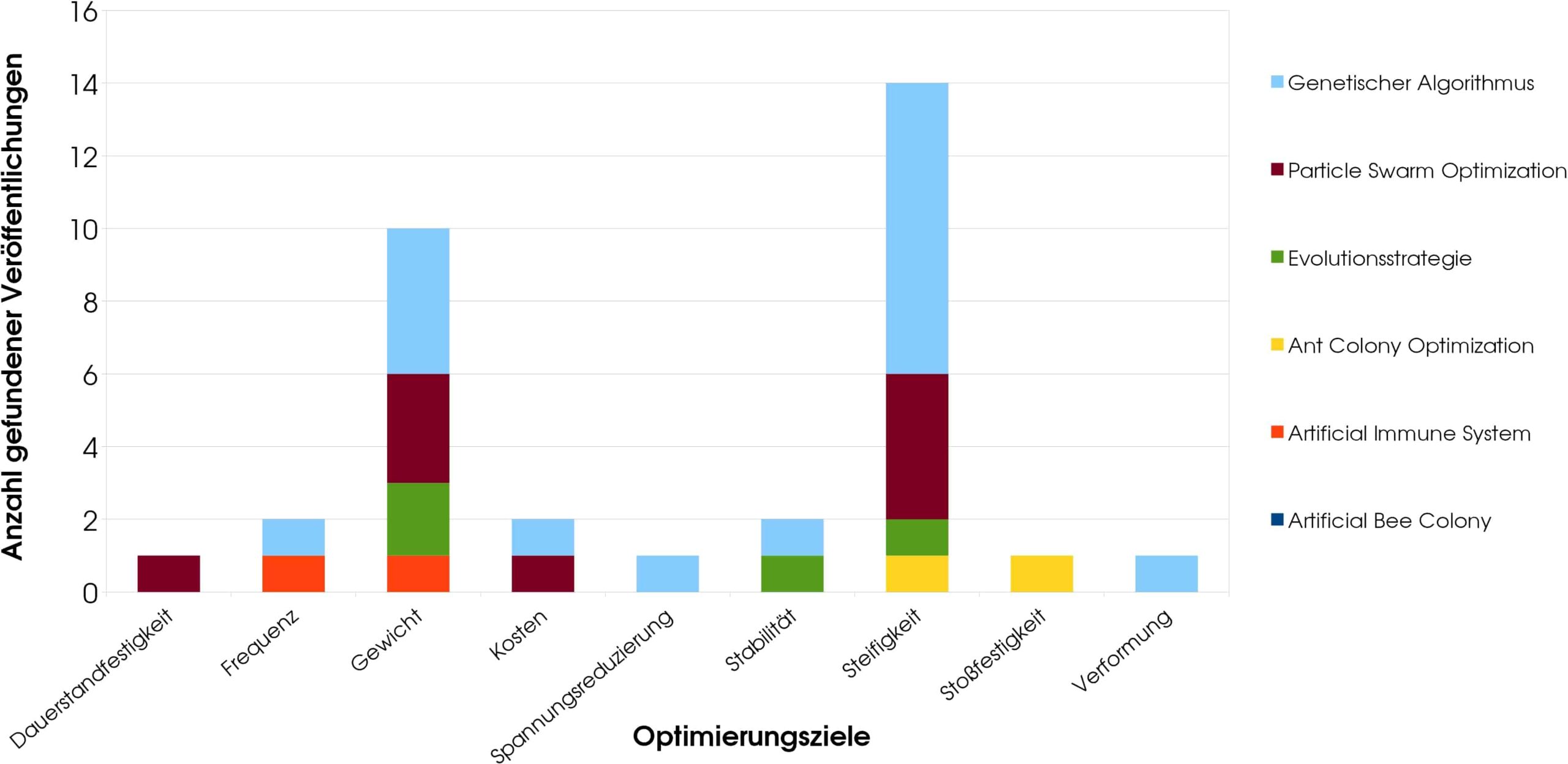
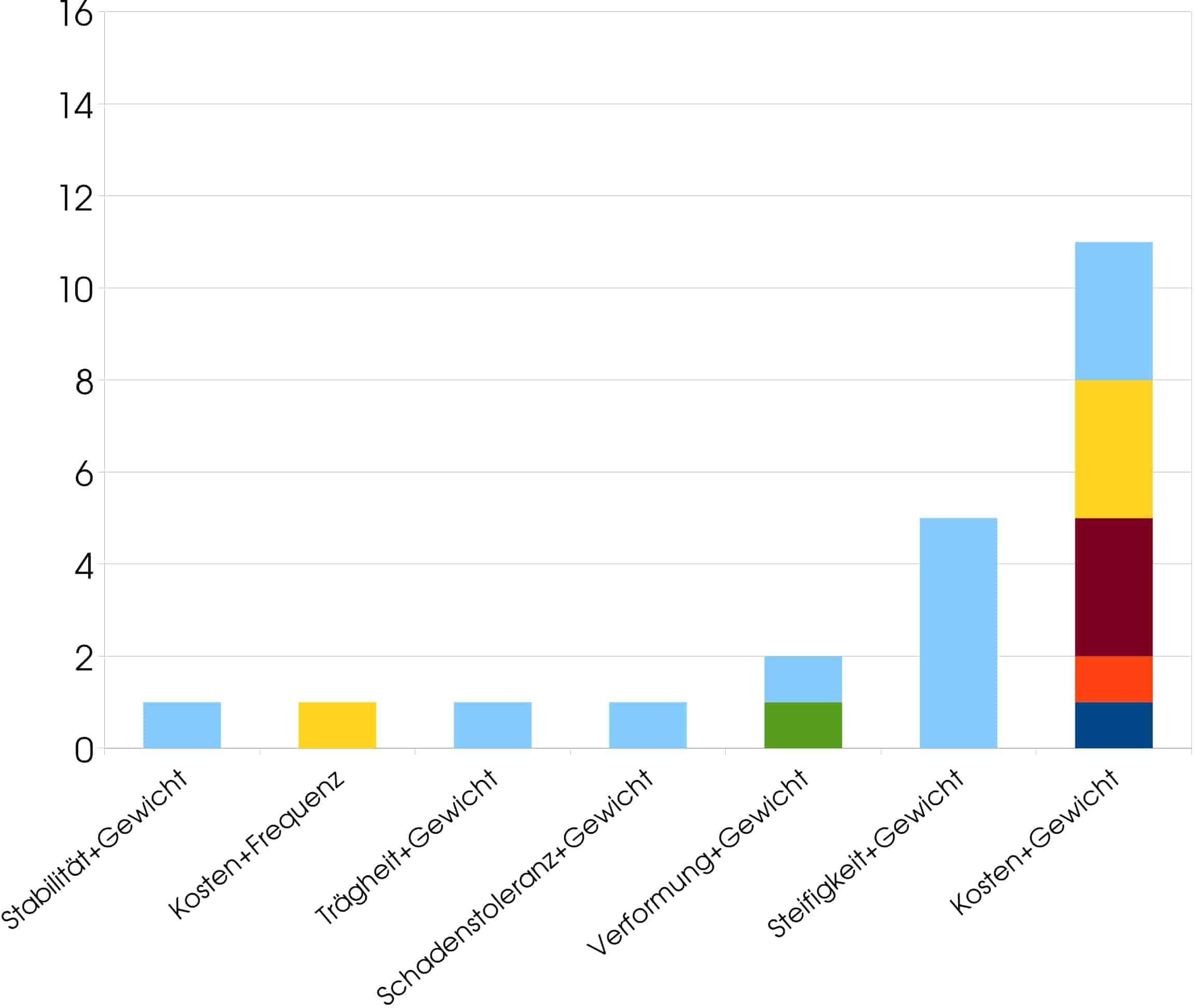
Es wurden insgesamt 56 Veröffentlichungen gefunden, die jeweils eine der genannten Optimierungsverfahren angewendet haben. Die Optimierungsziele hierbei waren: Dauerstandfestigkeit, Frequenz, Gewicht, Kosten, Spannungsreduzierung, Stabilität, Steifigkeit, Stoßfestigkeit, Verformung sowie, je einmal bei der Mehrzieloptimierung angewandt, Trägheit und Schadenstoleranz. Diese Optimierungsziele sind typisch für den Bereich des Maschinenbaus und daher nicht verwunderlich. Die Häufigkeit der angewandten Algorithmen ist sehr unterschiedlich und gleichfalls nicht sehr überraschend. Bei der einfachen Optimierung dominieren die Ziele Steifigkeit und Gewicht stark, was angesichts dessen, dass es sich hier um eine Leichtbautechnologie handelt, plausibel ist. Nicht zu erwarten war, dass das Ziel der Kosten wenig Beachtung findet, da doch die hohen Kosten eine der größten Herausforderungen bei Herstellung und Verarbeitung von Faserverbunden ist. Bei der Mehrzieloptimierung jedenfalls ist das anders; hier wird den Kosten gemeinsam mit dem Gewicht die größte Häufigkeit aller Optimierungsziele zuteil. Am zweithäufigsten ausgeprägt sind Steifigkeit und Gewicht. Die restlichen Zielkombinationen sind im Vergleich zu diesen beiden marginal.
Neben der Verwendungshäufigkeit der Optimierungsziele ist der Blick auf die Verwendungshäufigkeit der einzelnen Algorithmen zu richten. Mit 29 Anwendungen ist der GA der bei weitem meistverwendete. Die PSO folgt mit großem Abstand mit 12 Anwendungen, ACO mit 6, ES mit 5, AIS mit 3 und ABC mit einer einzigen Anwendung. In Tabelle 2 ist außerdem das Jahr der Entstehung sowie der Grad der Bekanntheit (nach eigener Einschätzung) aufgeführt. Dass der GA so häufig verwendet wird, hängt hauptsächlich mit seiner großen Bekanntheit zusammen; Die Popularität des GA geht soweit, dass er heute sogar teilweise synonym für jedwede naturanaloge algorithmische Optimierung verwendet wird und die meisten Ingenieure, auch wenn sie keinen Bezug zu algorithmischer Optimierung haben, den Begriff zumindest kennen. Ferner stellen sich zwei Auffälligkeiten heraus: Zum einen ist es bemerkenswert, dass die PSO der zweitjüngste Algorithmus aller hier behandelten ist, und aber schon am zweithäufigsten eingesetzt wurde. Zum anderen ist auffällig, dass die ES, die mit dem GA zusammen der erste naturanaloge Optimierungsalgorithmus überhaupt war, nur sehr selten angewendet wurde. Dass die Entwickler es versäumt haben die ES populär zu machen hatte zur Folge, dass er heute am ehesten in Deutschland, wo her herstammt, bekannt ist. Die ES braucht sich allerdings nicht hinter den anderen Verfahren verstecken, denn ganz im Gegenteil ist sie ihnen sogar einen sehr großen Schritt voraus: So wurde sie bereits intensiv von Mathematikern, Ingenieuren und Informatikern untersucht und in ihrer Leistungsfähigkeit immer wieder bestätigt, siehe dazu u.A. [3], [4]. Hier liegt sodann auch die Chance des „Underdog“, und zwar dass er nur wenig bekannt ist, zugleich aber eines der gefestigtsten Fundamente von allen hat.
| Algorithmus | Neuheit (Entstehung) | Bekanntheit (+/-) | Gefundene Veröffentlichungen |
|---|---|---|---|
| GA | 1970 | + | 29 |
| PSO | 1995 | – | 12 |
| ACO | 1992 | – | 6 |
| ES | 1970 | – | 5 |
| AIS | 1994 | – | 3 |
| ABC | 2005 | – | 1 |
Laminatoptimierung
Auswahl des Optimierungsalgorithmus
Aus den zur Disposition stehenden Verfahren, genannt in Kapitel 4, wird nun eines ausgewählt und hiermit eine Laminatoptimierung durchgeführt. In dieser Arbeit wird sich für die Evolutionsstrategie entschieden, da
- sie umfassend wissenschaftlich-empirisch ausgearbeitet und untersucht wurde
- sie in über 40 Jahren Forschungsarbeit verfeinert und weiterentwickelt wurde
- sie bisher nur selten zur Laminatoptimierung herangezogen wurde was ihrer Unbekanntheit zuzurechnen ist, aber ihrem Potential nicht gerecht wird
- die Evolution ein übergeordnetes Prinzip darstellt, das die meisten anderen natürlich-biologischen Mechanismen die in Optimierungsverfahren überführt wurden erst erklärbar macht.
Funktionsweise der Evolutionsstrategie
Die Evolutionsstrategie ist eine Heuristik. Heuristiken finden spätestens dann Anwendung, wenn deterministische Verfahren durch zu komplexe Problemstellungen nicht mehr zufriedenstellende Ergebnisse liefern können. Die ES macht sich das Prinzip der Evolution, und zwar jenes nach DARWIN zu eigen.
In dieser Arbeit werden (μ/ρ +, λ)-ES‘en verwendet (sprich: „mü durch rho plus komma lambda Evolutionsstrategien“). Dabei steht
- μ für die Anzahl der Eltern
- λ für die Anzahl an Kindern und
- ρ für die Anzahl an Rekombinanten, also die Anzahl an Eltern die sich miteinander kreuzen woraus ein Kind entsteht (in der Natur ist sie mit wenigen Ausnahmen gleich 2).
Zusätzlich muß eine Startschrittweite σS vorgegeben werden. Ausgehend von der vorliegenden Startkonfiguration werden nun μ neue Lösungen erzeugt, und zwar derart, dass die Veränderlichen variiert werden. Die Variierung erfolgt normalverteilt mit σS als Streumaß und 0 als Mittelwert. Im nächsten Schritt werden die Kinder erzeugt. Wenn ρ=1 ist, oder bei bestimmten anderen Parametereinstellungen erzeugen die Eltern die Kinder indem sie sich lediglich kopieren. Eine Andersartigkeit des Kindes wird dann allein durch Mutation seiner Gene generiert. Für ρ≠1 besteht das Kind aus gemischten Eltern-Genen die anschließend zusätzlich mutiert werden. Zu diesem Zeitpunkt existiert also eine Generation aus μ Eltern und λ Kindern. Für alle Eltern und Kinder (die in dieser Arbeit Laminate mit je verschiedenen Winkeleinstellungen repräsentieren) wird nun die Zielfunktion ausgewertet.
Der nächste Schritt ist die Selektion und entspricht in der biologischen Evolution dem „survival of the fittest“-Prinzip. Zunächst muß hierfür nach dem Strategietypus unterschieden werden, d.h. zwischen (+)-Strategie und (,)-Strategie. Er ist also ein binärer Eingabeparameter. Bei einer (+)-Strategie werden die Zielfunktionswerte der vorhandenen Eltern und Kinder miteinander verglichen. Diejenigen μ von ihnen mit den besten Zielfunktionswerten werden als Eltern für die neue Generation selektiert. Bei einer (,)-Strategie passiert genau dasselbe mit dem entscheidenden Unterschied, dass lediglich von den Kindern die neuen Eltern selektiert werden. Die Eltern einer Generation können bei (,)-Strategien also nicht für die nächste Generation als Eltern selektiert werden und nochmals an der Erzeugung neuer Kinder beteiligt sein. Für (,)-Strategien macht dies eine Eingabe von zwingend λ ≥ μ erforderlich; für (+)-Strategien gilt diese Einschränkung nicht.
Neben der Selektion der neuen Eltern passiert außerdem noch etwas sehr wichtiges, und zwar die Anpassung der Schrittweiten. Daß die folgenden Generationen die Variierung ebenfalls gemäß der Startschrittweite vornehmen ist nicht zweckmäßig, sondern sie muß fortwährend über den Optimierungsprozeß hinweg angepaßt werden. Dies kann verschiedenartig passieren. In dieser Arbeit kommen zwei fundierte Mechanismen zur Anwendung, und zwar die 1/5-Erfolgsregel und eine, die individuelle Schrittweitensteuerung betreibt, hier genannt „τ-Regel“. Die 1/5-Erfolgsregel ist nur bei (+)-Strategien anwendbar; ferner kann Rekombination nicht realisiert werden wenn sie zum Einsatz kommt. Die τ-Regel wiederum ist für beide Strategietypen und ebenfalls unter Verwendung der Rekombination einsetzbar. Siehe hierzu auch Kapitel 6.5 und Abb. 6. Die Gründe für diese unterschiedlichen Einsatzbereiche sind historisch bedingt. So waren (+)-Strategien die ersten Evolutionsstrategien; In diesem Stadium entwickelte man die 1/5-Erfolgsregel. (,)-Strategien und die Möglichkeit der Rekombination wurden später, und in diesem Kontext auch die τ-Regel entwickelt. Eine gute, ausreichend ausführliche Zusammenfassung über die Funktionsweise beider Schrittweitensteuerungsmechanismen findet sich z.B. in [7].
Dieser in diesem Kapitel beschriebene Prozeß setzt sich über mehrere Generationen, d.h. also Iterationsschritten fort. Am Ende der Optimierung stellt, je nachdem ob minimiert oder maximiert wird, jener Elter mit dem niedrigsten bzw. höchsten Funktionswert das optimale Ergebnis dar. Für tiefergehende Informationen über die Evolutionsstrategie siehe u.A. [4], [5], [6], [7], [8], [9], [10].
Optimierungskriterien
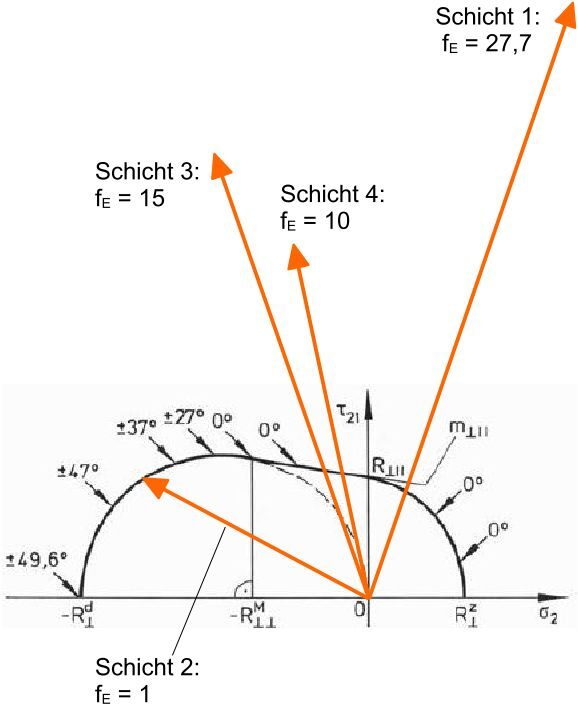
Damit optimiert werden kann muß ein System definiert vorliegen. Das ist die Startkonfiguration. Bei der Laminatoptimierung mit veränderlichen Winkeln der Einzelschichten ist die Startkonfiguration eine beliebig wählbare Winkelanordnung. Es müssen ferner Größen vorgegeben werden, die hieran variiert werden (sog. „Designvariablen“). Hier sind das die Ausrichtungen der Einzelschichten. Da es sich hier durch die Vorgabe diskreter Winkel um ein diskretes Optimierungsproblem handelt, muss diese Menge an Winkeln ebenfalls vorgegeben werden. Schließlich wird eine Zielfunktion aufgestellt die es zu minimieren oder maximieren gilt. Die Zielfunktion in dieser Arbeit ist, die maximale Anstrengung fE des zugehörigen Bruchmodus entsprechend dem CUNTZEschen Versagenskriterium zu minimieren. Hierfür wird für jede momentan eingestellte Laminatkonfiguration (d.h. die Winkel der Einzelschichten) der Beanspruchungszustand und alle 5 Versagensmodi ausgewertet. Jener Versagensmodus, der den kritischsten und damit höchsten Wert annimmt bestimmt die Zielfunktion, die es zu minimieren gilt. Die Optimierungsaufgabe besteht also formal darin, die optimale Winkelkonfiguration zu finden für die die maximale Anstrengung der am meisten beanspruchten Schicht minimal wird. Dies drückt die Optimierung der Ausrichtung aller Schichten und damit des gesamten Schichtaufbaus aus.
Von Interesse in dieser Arbeit ist insbesondere, wie sich die Parametereinstellungen der Evolutionsstrategie auf die Qualität des Ergebnisses auswirken und für welche Schichtanzahl welche Parameterkonfiguration geeignet ist. Da heuristische Optimierung stark wahrscheinlichkeitsbehaftet ist, werden in dieser Arbeit je Parametereinstellung und Schichtanzahl genau 100 Optimierungen durchgeführt. Das gemittelte Ergebnis gibt dann zuverlässig Aufschluß darüber, wie gut die Parametereinstellung gewählt war. Die Bewertung der Qualität des Ergebnisses wird aus zwei Merkmalen bestimmt: Wichtigstes Bewertungskriterium ist die Menge an gut gelungen Optimierungen, d.h. der Zuverlässigkeit. Es wird in dieser Arbeit eine Erfolgsquote von 80% festgelegt. Mindestens 80% von den 100 Optimierungen dürfen nicht mehr als 10% vom globalen Optimum abweichen (d.h. größer als 1,1 sein, siehe Kapitel 6.4). Darüber hinaus wird darauf geachtet, dass die gemittelte Anzahl der Funktionsauswertungen gering bleibt. Die Anzahl der Funktionsauswertungen ist ein Maß für die Geschwindigkeit und die benötigte Rechenkapazität des Algorithmus. Von allen Parameterkonfigurationen ist schließlich jene die beste, mit der die Erfolgsquote erreicht/überschritten wurde und im Mittel am wenigsten Funktionsaufrufe nötig waren.
Problemformulierung
Die Schichten des Laminats können drehbar veränderlich festgesetzt werden, was in dieser Arbeit gleichfalls die veränderlichen Parameter der Optimierung sind und oft eine der wenigen freien Variablen in der Laminatkonstruktion darstellen. Da in der industriellen Serienfertigung allerdings selten sämtliche Winkel verwirklicht werden können, wird sich gemeinhin auf eine Menge von diskreten Winkeln beschränkt. In diesem Modell wird folgende Menge von möglichen Winkeln festgelegt:
{0°, 15°, 30°, 45°, 60°, 75°, 90°, 105°, 130°, 145°, 160°, 175°}
Die Orientierung einer UD-Schicht ist also in 15°-Schritten im Bereich zwischen 0° und 180° veränderlich. Der Bereich zwischen einschließlich 180° und 360° braucht nicht definiert zu werden, da das Eigenschaftsprofil eines üblichen UD-Geleges zwei Symmetrieebenen hat, demnach beispielsweise eine Orientierung in 270° jener in 90° Orientierung entspricht.
Es gibt prinzipiell zwei Möglichkeiten eine Startkonfiguration zu bestimmen von der aus die Optimierung durchgeführt werden kann: Eine Möglichkeit ist jene, die in der Praxis in den allermeisten Fällen praktiziert wird da wenig oder keine Hinweise für eine gute Anfangskonfiguration vorliegen von der aus startend mit hoher Wahrscheinlichkeit das Optimum gefunden werden könnte; Diese erste Möglichkeit ist, die Startkonfiguration vollkommen willkürlich, das heißt zufällig zu bestimmen. Die andere Möglichkeit besteht darin, es dem Algorithmus am schwersten zu machen und die schlechtest mögliche Konfiguration vorzugeben damit der singuläre Fall einer vollkommen mißglückten Startkonfiguration simuliert wird. Diese zweite Möglichkeit wird in dieser Arbeit angewendet und damit das komplette Laminat um 90° gedreht, sodass die Belastung orthogonal zu den Fasern angreift. Der Wert der Zielfunktion beträgt in dieser Konfiguration gleich 27,7. Zwar gibt es andere Konfigurationen die noch schlechtere Zielfunktionswerte annehmen (z.B. komplette Laminatdrehung um 75° und 60° mit maximaler Anstrengung von 28,19 bzw. 34,60), da aber der Startpunkt durch eine 90°-Drehung am weitesten weg vom Optimum ist befindet er sich noch hinter diesen zusätzlich zu überwindenden Maxima.
Dadurch unterziehen wir dem Algorithmus den größtmöglichen Streßtest. Das bedeutet, dass die Zielfunktionslandschaft in beschwerlichstem Maße und auf längst möglichem Wege überwunden werden muß. Jene Ergebnisse also die das vorgegebene Qualitätsmaß erreichen, sind als herausragende Leistungen des Algorithmus anzusehen wenn bedacht wird, dass vom singulären „worst case“ gestartet wir und gleichwohl die Zielfunktion unstetig und partiell nicht differenzierbar ist (diskrete Wechsel des CUNTZEschen Bruchmodus sowie der betreffenden Einzelschicht).
In dieser Arbeit wird ein spezifischer und konstanter Belastungsfall Anwendung finden für den die Lösung bekannt ist. Das betrachtete Laminatmodell wird in dieser Arbeit einerseits monoaxial in Längs-Richtung gezogen und außerdem mit einem Biegemoment um die Achse in Faserrichtung belastet. Hinsichtlich des CUNTZEschen Versagens ist die hier betrachtete Beanspruchungssituation dahingehend normiert, dass bei optimaler Orientierung (wenn alle Schichten in 0° ausgerichtet sind) die Bruchbedingung gerade erfüllt ist und die Beanspruchung ihren zulässigen Maximalwert, der f0 = 1 ist, annimmt.
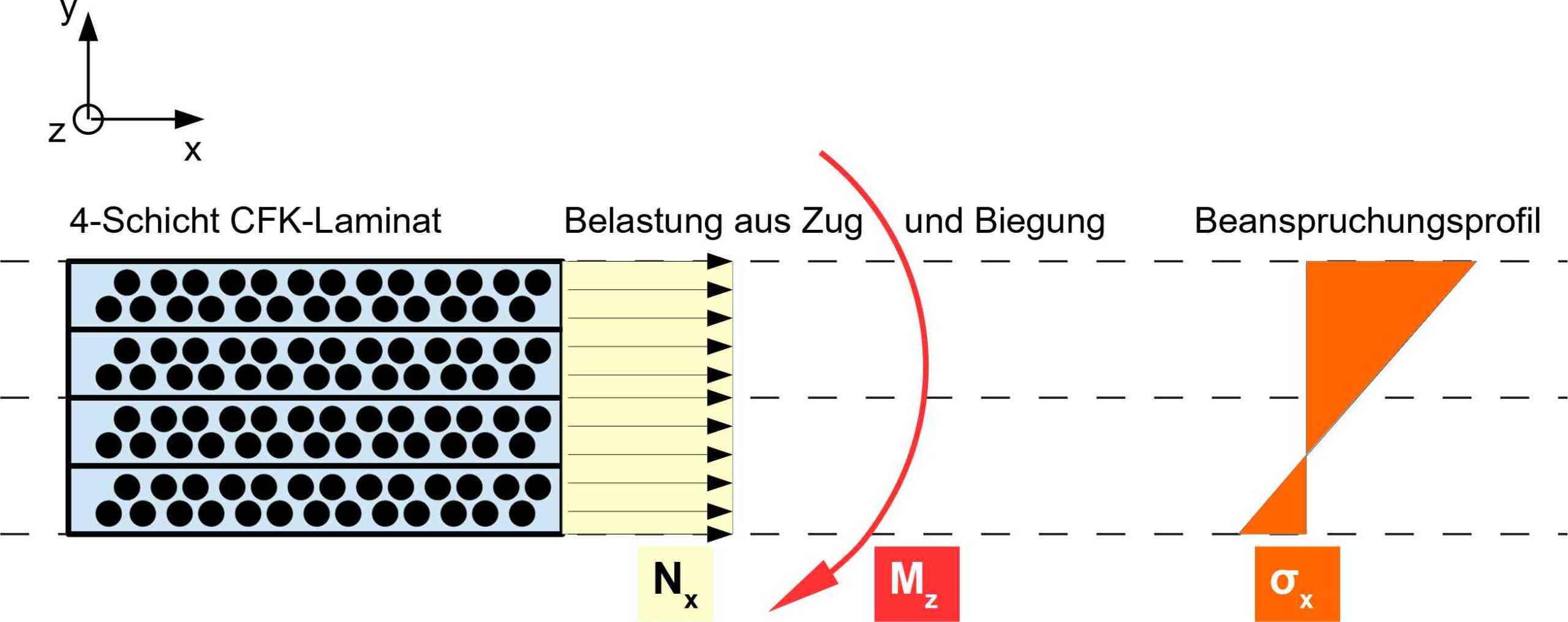
Durch dieses Belastungsprofil wird die oberste Schicht am stärksten beansprucht. Dies wird bewusst so gewählt damit die Schichten nicht symmetrisch und dadurch gleich belastet werden was in der Optimierung Redundanzeffekte hervorrufen könnte die bei der Auswertung und Bewertung stören würden. Dadurch, dass eine bestimmte Schicht bzw. bestimmte Schichten stärker belastet werden als andere, kann das Augenmerk auch darauf gerichtet werden, wie der Algorithmus mit der unterschiedlichen Sensitivität, die sich hieraus ergibt, umgeht. Eine Drehung der obersten Schichten hat demnach deutlich mehr Einfluß auf die Zielfunktion als die unteren. Gleichfalls soll der Algorithmus aber auch nicht abbrechen, wenn er die am stärksten Beanspruchten Schichten in die korrekte Position drehen konnte, sondern soll auch die Schichten korrigieren, die sich verglichen dazu geringer sensitiv auf die Zielfunktion auswirken.
Zunächst wird nach einer guten Parametereinstellung für ein Laminat mit einer Schichtanzahl von 4 gesucht. Eine niedrige Schichtanzahl gewährleistet, dass auf günstige Weise zunächst mit vielen Parametereinstellungen einigermaßen zwanglos experimentiert werden kann da die Rechenzeit gemeinhin in Maßen bleibt. Nachdem sich damit vertraut gemacht wird, wie das System auf unterschiedliche Eingaben reagiert, welche Eingaben die Zielfunktion stärker beeinflussen als andere und wie schnell und zuverlässig die Optimierung mit einzelnen Parameterkonfigurationen ist, wird das Laminat nach oben skaliert. Dies geschieht durch eine Erhöhung der Anzahl an Einzelschichten auf zunächst 8 und anschließend 12. Die Erkenntnisse aus der Optimierung des 4-schichtigen Laminats sollen als richtungsweisend und als Unterstützung bei höherskalierten Laminaten dienen, wenngleich man sich bewusst sein muß, dass sich die Zielfunktion mit deutlich steigenden Schichtanzahlen stark verändert. Sie wird nicht nur quantitativ durch die steigende Anzahl an möglichen Winkelkonfigurationen komplexer sondern auch qualitativ differenzierter und hochmodaliger (mehr lokale Optima). Dies macht es nötig, die Parameterkonfiguration jedes Mal aufs Neue zu definieren.
Parameterstudien
Das vorliegende Optimierungsmodell hat insgesamt 9 Eingabeparameter:
- Anzahl Eltern: μ ∊ ℕ>0
- Anzahl Kinder: λ ∊ ℕ>0
- Strategietypus: (+) oder (,)
- Startschrittweite: σS ∊ ℝ>0
- Mutative Schrittweitenregelung (MSR): 1/5-Erfolgsregel oder τ-Regel
- MSR-Parameter der τ-Regel: τ1 und τ2 ∊ {0,1} ∊ ℝ
- Anzahl der zu kreuzenden Eltern: ρ ∊ {1,μ} ∊ ℕ
- Abbruchkriterium ε ∊ {0,1} ∊ ℝ>0
Es sind jedoch nie alle Parameter für eine Optimierung einzugeben, sondern hängen von der Strategie ab und bedingen einander. So hat eine (+)-Strategie je nachdem mit welcher MSR operiert wird genau 4 oder 7, sämtliche (,)-Strategien immer genau 7 Eingabeparameter.
Die Parameter haben verschieden gewichtigen Einfluß auf den Optimierungsprozeß und erfüllen unterschiedliche Aufgaben. Manche sind global und übergeordnet und manche sehr spezifisch auf Teilfunktionen bezogen. Sie sind, sowohl was ihre Wichtigkeit in der Erfüllung ihrer Aufgaben als auch ihr Maß an Einwirkung in den Optimierungsprozeß und damit sein Resultat angeht, nicht als ebenbürtig zu betrachten.
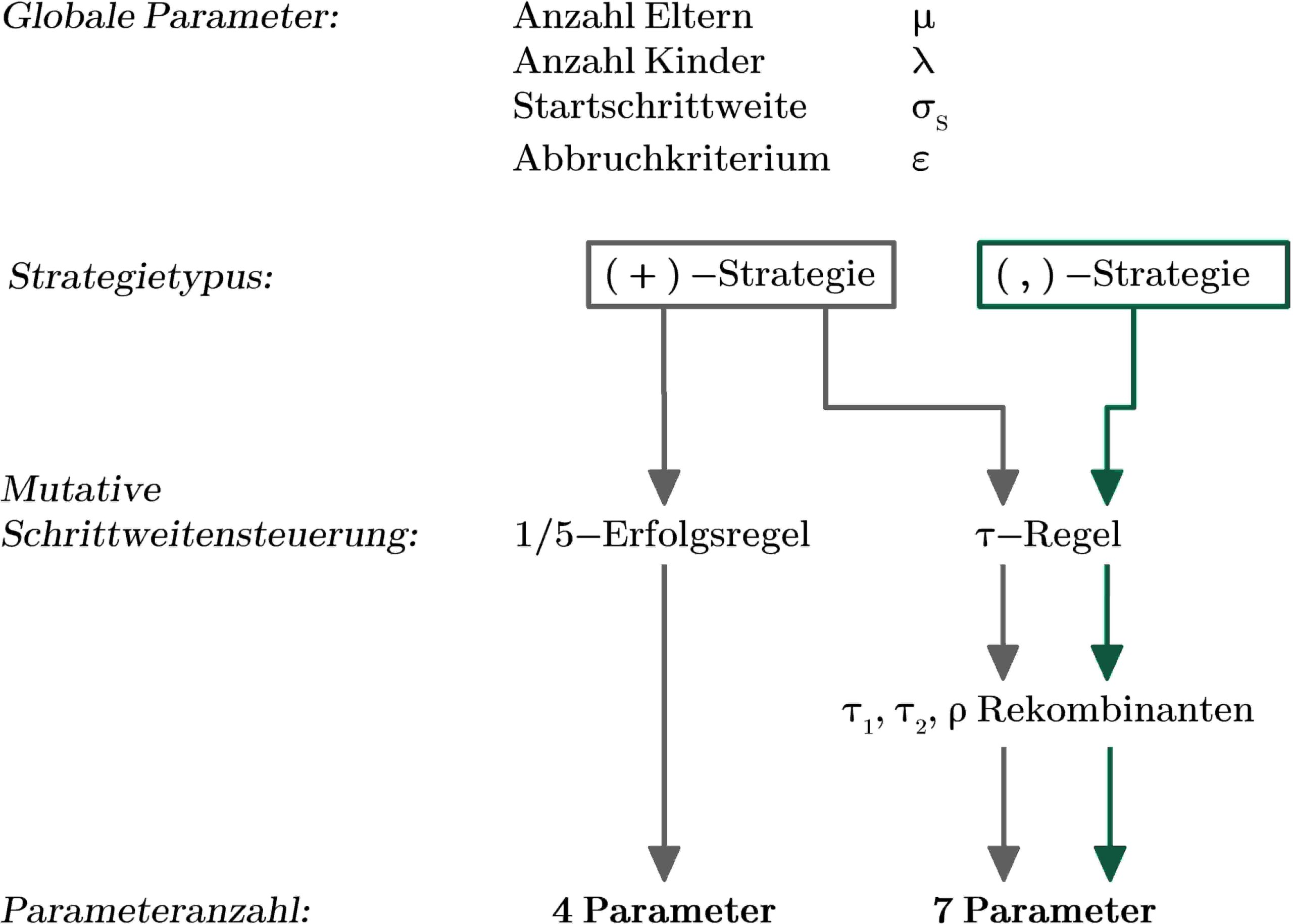
Die Menge von, global betrachtet, 9 Eingabeparametern haben Wertebereiche die mehrheitlich unendlich groß sind (reelle Zahlen allgemein bzw. ganze Zahlen ohne obere Schranke). Von einigen unterschiedlichen und erwähnenswerten Ansätzen wird sich in dieser Arbeit aus zwei Gründen dafür entschieden, zunächst mit (+)-Strategien und 1/5-Erfolgsregel als MSR zu arbeiten. Mit einer solchen ES gibt es die geringste Anzahl möglicher Eingabeparameter, weshalb mit ihr ein guter erster Entwurf einer Parameterkonfiguration gelingen kann. Ferner kann sie dabei helfen, Aussagen über die Beschaffenheit der Zielfunktion zu treffen, was für die Parametereinstellungen anderer ES’en dienlich sein wird. Zum Beispiel kann mit dem Konvergenzverhalten einer (1+1)-ES mit niedrigen Startschrittweiten die nähere Umgebung der Zielfunktion ausgehend von der Startkonfiguration ausgelotet werden; Wird nach wenigen Iterationen ein lokales Optimum gefunden, hat man Aufschluß über seine Existenz (es existiert), seine Ausprägung (Funktionswert wiedergeben lassen) sowie seine ungefähre Entfernung (nah).
Je komplexer, z.B. verrauschter und hochmodaler die Zielfunktion ist, desto mehr ist die (+)-Strategie der (,)-Strategie im Auffinden globaler Optima unterlegen, jedoch betreffend der Geschwindigkeit und Konvergenzsicherheit überlegen, was weitere Gründe sind, sich zunächst mit ihr zu beschäftigen.
Die 1/5-Erfolgsregel ist die ältere der beiden MSR und hat durch ihre Plakativität („im Mittel genau eine erfolgreiche Mutation von fünfen“) aber nicht weniger durch ihre wissenschaftliche Ausarbeitung und Begründung relativ große Berühmtheit erlangt. Auch aus dem Umstand heraus, dass sie, als sie vor über 40 Jahren herausgearbeitet wurde eine der frühesten selbstadaptiven Mechanismen war und bis heute unverändert geblieben ist, ist sie in dieser Arbeit von Interesse.
Die Komplexität beider Strategietypen, sowohl (+)- als auch (,)-Strategie, sind mit der Verwendung der anderen MSR, der τ-Regel, gleich. Dennoch wird als nächster Schritt weiterhin mit der (+)-Strategie in Verbindung mit der τ-Regel operiert werden, und zwar weil (+)-Strategien schneller sind als (,)-Strategien. Solange mindestens 80% erfolgreicher Optimierungen mit einer (+)-Strategie erreicht werden können, ist eine (,)-Strategie nicht nötig und wird in der Regel länger brauchen. Erst wenn nur noch mit sehr großen Parametern unter Verwendung der (+)-Strategie Erfolge erzielt werden können bzw. im Umkehrschluß gesprochen diese unverhältnismäßig lange brauchen, werden (,)-Strategien in dieser Arbeit Anwendung finden.
Die Menge von 7 Parametern denen man ausgesetzt ist wenn die 1/5-Erfolgsregel nicht zur Anwendung kommt, ist zu groß um allen gleiche Beachtung schenken zu können. Von zentraler Bedeutung sind die 3 übergeordneten und in jeder Strategie zur Anwendung kommenden Größen der Anzahl der Eltern, der Kinder sowie die Startschrittweite. Für sie gibt es gemeinhin wenig Empfehlungen oder Richtwerte an denen man sich orientieren kann. Ihre wichtigsten Bedeutungen sind wie folgt: Je mehr Eltern erzeugt werden, desto größer ist die Wahrscheinlichkeit das globale Optimum zu finden, was allerdings zu Lasten der Geschwindigkeit geht. Je größer die Anzahl der Kinder gewählt wird, desto sicherer konvergiert der Algorithmus, was ebenfalls durch eine aufwändigere Prozedur erkauft wird. Eine Empfehlung zur Einstellung des Verhältnisses von Eltern zu Kindern gibt [6] ab, wonach es etwa bei 1:7 liegen sollte. Dies ist in dieser Arbeit als Orientierung dienlich; es wird allerdings auch deutlich davon abgewichen werden. Es gilt: Je kleiner dieses Verhältnis ist, desto größer ist der „Selektionsdruck“. Ein großer Selektionsdruck heißt, dass wenig Toleranz gegenüber schlechteren Lösungen besteht. Praktisch bedeutet das, dass die Konvergenzsicherheit und die Geschwindigkeit mit steigendem Selektionsdruck gleichfalls steigen, aber die Wahrscheinlichkeit sinkt, das globale Optimum zu finden. Je gutmütiger das zu optimierende System ist, desto zulässiger sind große Selektionsdrücke. Siehe hierzu auch [7].
Was gut eingestellte Startschrittweiten betrifft, so hängen sie wesentlich mit dem Startpunkt, der Beschaffenheit der Zielfunktion aber auch mit der restlichen Gesamtkonstitution des Systems zusammen. Es ist sich danach zu orientieren, wie groß der Vektor der Designvariablen ist, denn zu diesem muß sie verhältnismäßig sein. In dieser Arbeit hat der Vektor die Länge 12 (0° 15° 30° 45° …). Es ist also wenig sinnvoll und hat wenig Aussicht auf Erfolg, Startschrittweiten von etwa 10 bis 12 oder von 0,1 bis 0,7 zu wählen. Erstere spannt fast den ganzen Vektor auf wodurch die Normal- zur Gleichverteilung degeneriert und letztere trägt der Vektorlänge nicht Rechnung wodurch zu viele Elemente zu Beginn der Optimierung ignoriert werden. Insbesondere dadurch, dass von der schlechtest denkbaren Konfiguration gestartet wird, ist es am Beginn entscheidend, hinreichend große Schrittweiten zu haben. In dieser Arbeit wird mit ganzzahligen Startschrittweiten zwischen 1 und 8 gearbeitet werden.
Bei der Anwendung der τ-Regel treten drei zu definierende Faktoren in Erscheinung, und zwar τ1, τ2 und die Anzahl der Rekombinanten ρ. Wenngleich es nicht uninteressant wäre, den Einfluß der Parameter τ1 und τ2 zu untersuchen, wird, abgesehen von ein paar wenigen Tests dies in dieser Arbeit nicht geschehen. Zum einen liegt der Grund darin, dass τ1 und τ2 geringen Einfluß haben und sich auf Konvergenzverhalten, Geschwindigkeit und Zuverlässigkeit nur wenig auswirken. Zum anderen sind diese beiden Größen Ausnahmen im Parameterpool von ES’en dahingehend, da für sie Empfehlungen in der Fachliteratur abgegeben wurden denen sich in dieser Arbeit bedient wird. So empfiehlt [6], beide zwischen 0,1 und 0,2 festzulegen. τ1 wird in dieser Arbeit mit 0,1 und τ2 mit 0,2 festgelegt.
Ein im Gegensatz dazu wichtiger Faktor ist ρ, der ein Maß für die Vermischung der Individuen ist. Wenn keine Rekombination stattfindet, ρ also gleich 1 ist, erzeugt der Elter ein Kind aus sich selbst heraus mit geänderter Konfiguration gemäß aktueller Schrittweite und der Normalverteilung. Wenn sich Eltern (zwei wie man es aus der Natur kennt oder bis zu sämtlich vorhandene) kreuzen, werden zunächst vollkommen zufällig ihre Konfigurationen vermischt und diese anschließend, wie oben, gemäß Schrittweite und normalverteilter Wahrscheinlichkeit variiert. ρ wird in dieser Arbeit im Wesentlichen mit 3 Einstellungen verwendet werden, und zwar mit
- 1, wodurch die Qualität von Kreuzung allgemein abstrahiert werden soll,
- 2, um die übliche „natürliche“ Kreuzung abzubilden sowie
- μ, der den Extremwert markiert.
Das Abbruchkriterium ε ist das Verhältnis von der Fitness (bedeutet: Wert der Zielfunktion) des Besten einer Generation zum Mittel der Fitness aller Eltern und Kinder dieser Generation. Es wird gemeinhin zwischen 0,7 und 0,99 eingestellt, was von verschiedenen Faktoren abhängt. Am Wesentlichsten wird geprüft, wie viele Optimierungen einer 100-maligen Studie die hier festgelegte globale Abbruchschranke von 80 Generationen erreicht. Wird sie erreicht, wird das als nicht konvergiert eingestuft. Wenn hierbei allerdings dennoch gute Resultate hervortraten, kann davon ausgegangen werden, dass das Abbruchkriterium zu gutmütig eingestellt ist. Nachdem es in diesen Fällen nachjustiert und korrigiert wird, bleiben meist die guten Ergebnisse erhalten mit gleichzeitig sinkenden benötigten Generationen. ε ist also ein Parameter, der zunächst groß eingestellt wird (z.B. 0,95 oder 0,99). Sofern die Ergebnisse gut sind aber diverse bis viele Optimierungen bis zur globalen Abbruchsschranke dauern, wird ε dann für den nächsten Versuch mit ansonsten gleichen Parametern herunterskaliert. Auf diese Weise wird das Verhältnis von erfolgreichen, gültigen Optimierungen je Studie und geringen benötigten Funktionsauswertungen austariert.
Ergebnisse
Nach oben beschriebener Vorgehensweise wurden Ergebnisse erhalten, die in Tabelle 3 und Tabelle 4 sowie in Abb. 7 zusammengefasst wiedergegeben werden.
| Parameter | 4 Schichten | 8 Schichten | 12 Schichten |
|---|---|---|---|
| Strategie | (1 + 20) | (10 + 50) | (8 , 60) |
| Startschrittweite σS | 6 | 3 | 3 |
| MSR | 1/5-Erfolgsregel | 1/5-Erfolgsregel | τ-Regel |
| τ1 | – | – | 0,1 |
| τ2 | – | – | 0,2 |
| Rekombinanten ρ | – | – | 8 |
| Abbruchkriterium ε | 0,95 | 0,75 | 0,85 |
| Einzelergebnisse | 4 Schichten | 8 Schichten | 12 Schichten |
|---|---|---|---|
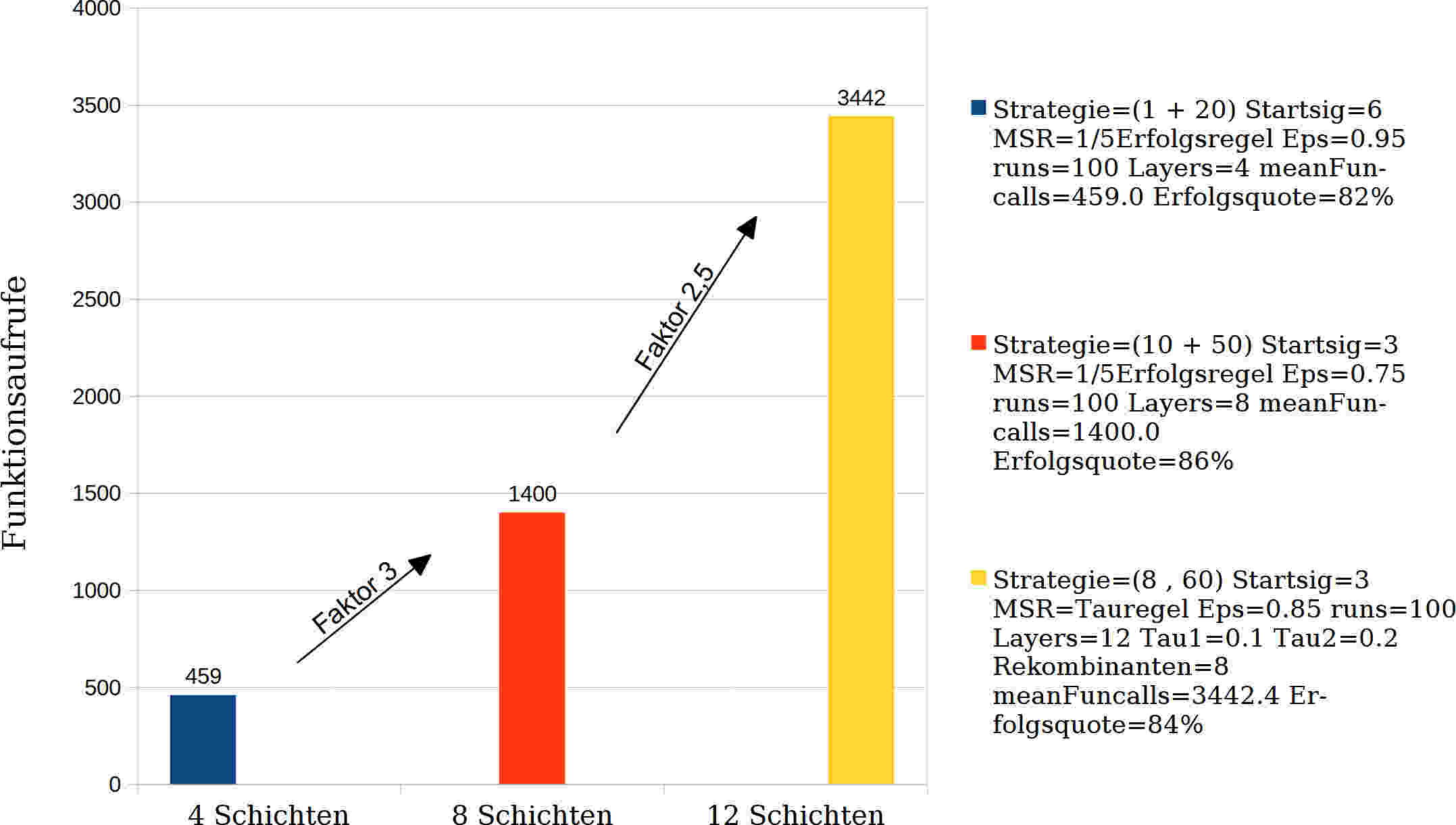
| Mittlere Anzahl Funktionsaufrufe | 459 | 1400 | 3442 |
| Mittlere benötigte Generationen | 24 | 29 | 58 |
| Mittlerer Funktionswert | 1,18 | 1,095 | 1,07 |
| Mittlere Berechnungszeit | 0,8s | 4,3s | 30s |
| Nicht konvergierte Optimierungen | 0 | 0 | 13 |
| Erfolgsquote | 82% | 86% | 84% |
Bei der Ermittlung der Parameter wurde, wie erwartet erkannt, dass die Einstellung der Startschrittweite sehr großen Einfluß auf das Ergebnis hat. Startschrittweiten von grösser 4 und kleiner 3 waren in den Versuchen üblicherweise nicht sinnvoll. Das 4-schichtige Laminat mit bester gefundener Startschrittweite von 6 ist eine Ausnahme. In allen anderen Fällen sank die Erfolgsquote mit Startschrittweiten größer 4 und kleiner 3 mit größer werdenden Abweichungen.
Ferner wurde bei den 4- und 8-schichtigen Laminaten unter Verwendung der 1/5-Erfolgsregel wesentlich bessere Resultate registriert als unter Verwendung der alternativen τ-Regel, und zwar sowohl bei (+)- als auch bei (,)-Strategien. Bei dem 12-schichtigen Laminat erzielten Strategien unter Verwendung der 1/5-Erfolgsregel ebenfalls gute Ergebnisse. Sie fanden sogar in den überwiegenden Fällen deutlich verlässlicher das Optimum mit vertretbarer Laufzeit (d.h. vertretbare Anzahl mittlerer benötigter Funktionsaufrufe). Dabei war zu registrieren, dass sich Abweichungen von Parametereinstellungen relativ robust und gutmütig gegenüber den Ergebnissen verhielten, was als positiv zu werten ist. Von allen drei Strategietypus/MSR-Kombinationen schnitten (+)-Strategien unter Verwendung mit der τ-Regel am schlechtesten ab. Die Qualität ihrer Ergebnisse ist meist zwar gut, der Algorithmus zeigt aber große Konvergenzprobleme. Dies hat damit zu tun, dass es problematisch ist die τ-Regel auf (+)-Strategien anzuwenden da sie hier versagen kann. Siehe dazu Kapitel 8.
Trotz der guten Ergebnisse die auch für das 12-schichtige Laminat mit (+)-Strategien in Kombination mit der 1/5-Erfolgsregel erzielt wurden, gab es für dieses mit einer (,)-Strategie das beste Resultat. Dies war, aufgrund des Charakters von (,)-Strategien, der für schwierige Zielfunktionen konzipiert wurde, erwartet worden. Da davon auszugehen ist, dass der Komplexitätsgrad der Zielfunktion eines Laminats mit zunehmender Schichtanzahl mindestens exponentiell steigend verläuft, läßt das den Einsatz von (,)-Strategien in gleichem, zunehmenden Maße gerechtfertigt und schließlich nötig werden.
Als überaus bedeutsam hat sich der Faktor der Rekombination herausgestellt. Strategien ohne Rekombination, also mit ρ=1, hatten gemeinhin die schlechtesten, Strategien mit ρ=2 deutlich bessere und Strategien mit ρ=μ die mit Abstand besten Resultate je Konfiguration. Voraussetzung hierfür war allerdings, dass die Anzahl an Eltern und Kindern sowie die Startschrittweite hinreichend eingestellt waren. Ein Rekombinationsfaktor von ρ=μ kann, wie sich auch gezeigt hat, unzureichende Einstellungen dieser genannten Größen nicht wettmachen. Es sei allerdings erwähnt, dass in dieser Arbeit nur punktuell über eine Elternanzahl von μ=10 hinaus Versuche durchgeführt wurden. Die Gültigkeit der Beobachtungen über diese Anzahl hinaus ist nicht mehr oder nur noch eingeschränkt gegeben.
Was den Selektionsdruck zu den hier durchgeführten Untersuchungen zur Laminatoptimierung betrifft, so hat sich herausgestellt, dass bei hinreichender Populationsgröße mit dem Verhältnis von Eltern zu Kindern von 1:7 was in [6] als Empfehlung genannt wird, tatsächlich gute Resultate erzielt wurden. Es wird hiermit als Richtwert für eine Laminatoptimierung ebenfalls empfohlen.
Bezüglich des Abbruchkriteriums ε hat sich herausgestellt, dass dessen optimale Einstellung nicht, oder zumindest nur sekundär von der Schichtanzahl abhängt, sondern dass sie strategieabhängig ist und für jede einer solchen neu eingestellt werden muß. Diese Erkenntnis ist auch plausibel, da zwar auch die Beschaffenheit der Zielfunktion und insbesondere des Optimums Einfluß auf das Konvergenzverhalten der Strategie haben. Das Populationsverhalten, allgemein und in der Nähe des Optimums, ist aber von Strategie zu Strategie unterschiedlich was jedes Mal ein aufs Neue angepasstes ε erfordert. Eine Gesetzmäßigkeit ist hiervon nicht ableitbar.
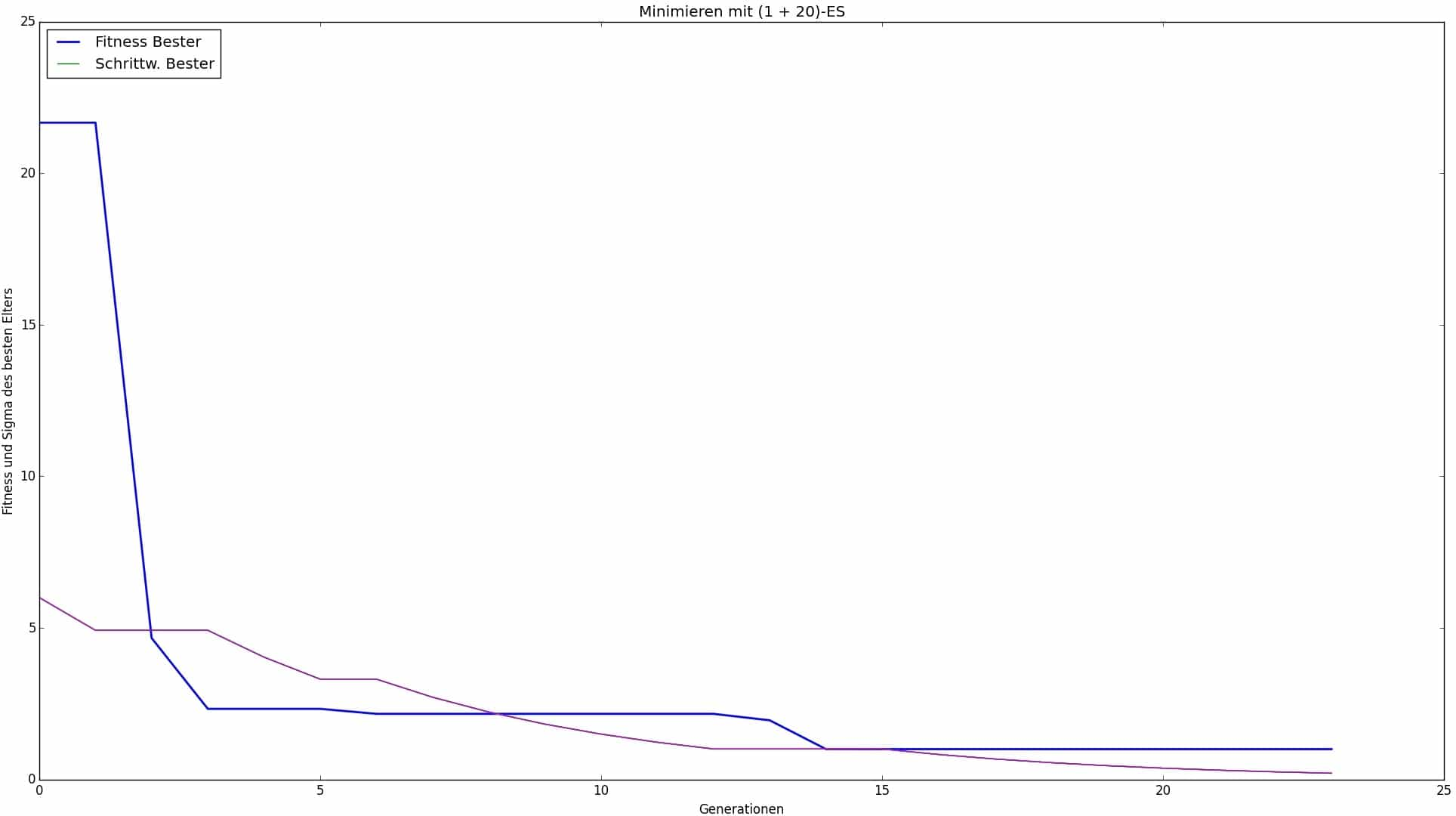
Abb. 8: Eine Optimierung eines 4-Schicht-Laminats mit Parameterkonfiguration nach Tabelle 3
Diskussion
Vorneweg sei daran erinnert, dass diese Untersuchungen zur Laminatoptimierung ein worst-case-Szenario sind, für das ein katastrophal mißlungenes Laminatdesign als Startkonfiguration verwendet wurde. Es sind demnach deutlich bessere Ergebnisse als auch gutmütigeres Verhalten des Algorithmus auf die Parametereingaben zu erwarten wenn mit einer zufällig generierten Startkonfiguration begonnen wird, wie es auch in der Praxis üblich ist. Die wichtige Maxime, dass eine hinreichend gute Startkonfiguration vorliegen muß damit das Potential des Optimierungsverfahrens voll ausgeschöpft werden kann, wurde in dieser Arbeit bewusst strapaziert. Neben der Laminatoptimierung die durchgeführt wurde, stellte diese Maßnahme gleichzeitig ein Leistungstest des Algorithmus dar.
Die Ergebnisse zeigen, dass bei niedrigen Schichtanzahlen die (+)-Strategie in Verbindung mit der 1/5-Erfolgsregel vollkommen ausreicht und sie sogar die mit Abstand besten Ergebnisse liefert sowie am sichersten konvergiert. Erfreulich für den Anwender ist, dass sie auch die wenigsten Parameter zur Eingabe verlangt und man mit ihr daher bei niegrigzahligen Mehrschichtverbunden unter hier untersuchten Gegebenheiten nicht sehr viel falsch machen kann. Es ist definitiv zulässig und empfehlenswert, zunächst mit nur einem oder wenigen Eltern und relativ vielen Kindern zu operieren da hiermit bereits beachtliche Ergebnisse erzielt werden können.
Von entscheidender Bedeutung ist die Wahl der Startschrittweite, die auf die Länge des Vektors der die Designvariablen trägt abgestimmt sein muß. Hier war der Designvariablen-Vektor jener, der die Winkel beinhaltete und hatte demnach die Länge 12. Gelungene Startschrittweiten lagen also bei 3 und 6, die 25 bzw. 50 % der Länge entsprechen. Dies sei sowohl als Richtwert bei der Optimierung höherskalierter Laminate empfohlen als auch bei Designvariablen-Vektoren größerer oder kleinerer Länge. Im Zweifel seien kleinere Startschrittweiten zu bevorzugen, da sich mit zufälliger Startkonfiguration i.d.R. alle Schichten näher am Optimum befinden als es in dieser Arbeit der Fall war. Dass sich diese hier ermittelten Startschrittweiten im linken bis mittleren Bereich des Vektors befinden hängt damit zusammen dass sich der optimale Schichtwinkel, der in dieser Arbeit bekannt und für alle Schichten gleich war (0°), in der Implementierung etwas weiter links von der Mitte befand. Da die optimalen Winkel normalerweise nicht bekannt sind und diese an beliebiger sowie je Einzelschicht unterschiedlicher Stelle im Vektor stehen können, stellt dies also keine Gesetzmäßigkeit dar.
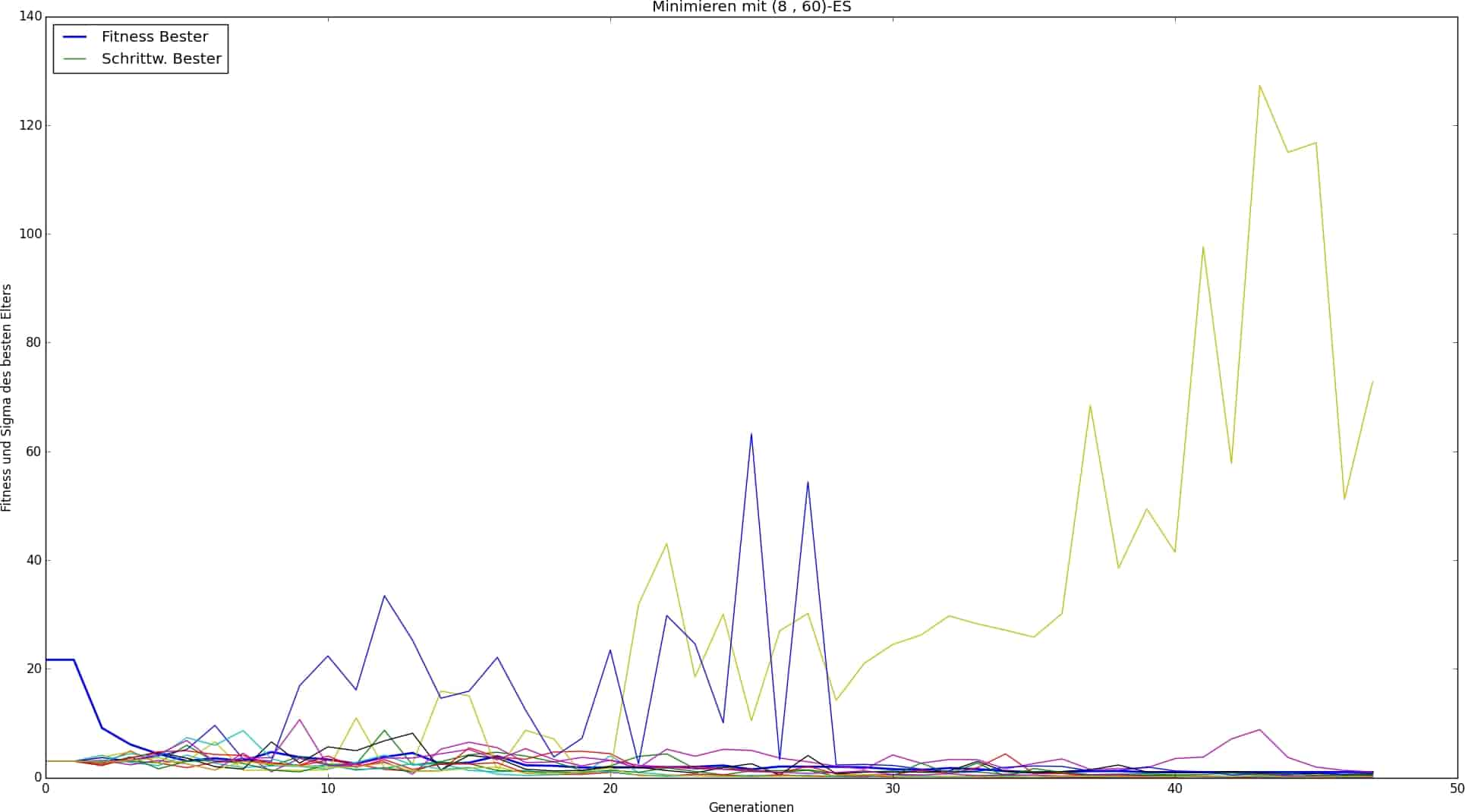
(,)-Strategien sind deutlich weniger konvergenzsicher und hinsichtlich ihrer zu tätigen Einstellungen sensitiver. Dies hat sich in dieser Arbeit bestätigt. (,)-Strategien sollten i.A. bei niedrigzahligen Mehrschichtverbunden vermieden werden. Sie spielen ihren Vorteil bei hohem Komplexitätsgrad aus und erkaufen ihn sich mit ihrer hohen Sensibilität was Dauer der Optimierung, Konvergenzsicherheit, Parameteranzahl und Parametereinfluß betrifft. Exemplarisch ist das an dem 12-schichtigen Laminat mit Einstellungen gemäß Tabelle 3 zu erkennen, dessen Optimierungsverlauf in Abb. 10 dargestellt ist. Dass hier zwei Schrittweitenwerte stark ausbrechen von dem sich einer bis zum Abbruch nicht mehr reduziert ist ein Anzeichen dafür, dass das Konvergenzverhalten instabil ist. Es sei darauf hingewiesen, dass sich per Feineinstellung aller Parameter das Konvergenzverhalten für eine bestimmte (und diese) Strategie verbessern ließe. Dies hätte hier aber nur kosmetische Bedeutung, da die erzielten Resultate vollkommen zufriedenstellend sind.
(+)-Strategien unter Verwendung der τ-Regel waren in dieser Arbeit die problematischsten unter allen betrachteten. Sie sind nur sehr selten konvergiert, was auch ihrer strukturellen Schwäche geschuldet ist. Dies wird z.B. auch von [7] hervorgehoben. Bildlich läßt sich diese Schwäche wie folgt beschreiben: Wenn z.B. ein Elter eine relativ gute Qualität aufweist, ist er also in der Nähe eines lokalen Optimums. Wenn er von dort aus mit aktuell relativ großen Schrittweiten Kinder erschafft, aber in dieser Entfernung weit und breit keine besseren Funktionswerte vorhanden sind, werden diese dann praktisch nie ausgewählt (da sie immer schlechtere Qualitäten aufweisen). Ferner passt sich die Schrittweite des Elters dadurch auch nicht mehr an (was durch das Erzeugen eines erfolgreicheren Kindes geschehen würde und die Auswechslung des Elters zur Folge hätte). Das Ergebnis ist ein quasi unendlicher und erfolgloser Fortschritt. Es kann aber dennoch mit (+)-Strategien unter Verwendung der τ-Regel gearbeitet werden. Um sie zu verwenden muß ein anderes Abbruchkriterium als das hier definierte festgelegt werden. Sinnvoll ist beispielsweise ein Abbruch nach einer Bestimmten Anzahl von Generationen oder das Maß, für wie viele Generationen rückwirkend keine Verbesserung (heißt: Auswechslung) des Besten mehr eintrat. Als Kompensation für ihr strukturelles Defizit ist anzuraten, mit hoher Anzahl von Kindern zu operieren um die Wahrscheinlichkeit zu erhöhen, sich von relativ geringwertigen Positionen wieder zu lösen. Ferner seien eher geringe denn hohe Startschrittweiten empfohlen.
Der Faktor, der den erhöhten Rechenaufwand mit steigender Schichtanzahl und optimalen Einstellungen nach Tabelle 3 wiedergibt, beträgt zwischen einem 8-schichtigen und einem 4-schichtigen Laminat mit 1400 Funktionsaufrufe / 459 Funktionsaufrufe = 3. Jener zwischen einem 12-schichtigen und einem 8-schichtigen Laminat beträgt mit 3442 Funktionsaufrufe / 1400 Funktionsaufrufe = 2,5. Im Gegenzug beträgt der Faktor der die Steigerung der möglichen Winkelkonfigurationen und damit auch möglicher Lösungen von 4 auf 8 und von 8 auf 12 Schichten wiedergibt 128 / 124 = 1212 / 128 = 124 = 20736.
Dies zeigt deutlich, dass per Evolutionsstrategien und lediglich zu variierenden Parametereinstellungen enorme Komplexitätssteigerungen und -grade beherrscht werden können. Sie ist also ausdrücklich für die Laminatoptimierung geeignet und sollte ebenfalls für anderweitige komplexe Optimierungsaufgaben von FVK erwogen werden.
Literatur
[1] Schürmann, Helmut: Konstruieren Mit Faser-Kunststoff-Verbunden. 2. Aufl.. Berlin Heidelberg New York: Springer-Verlag, 2007.
[2] Cuntze, R. u.A.: Neue Bruchkriterien und Festigkeitsnachweise für unidirektionalen Faserkunststoffverbund unter mehrachsiger Beanspruchung: Modellbildung und Experimente; BMBF-Förderkennzeichen 03N8002; Abschlußbericht 1997. Düsseldorf: VDI-Verlag.
[3] Born, J.: Evolutionsstrategien zur numerischen Lösung von Adaptionsaufgaben; Dissertation an der Humboldt-Universität, Berlin, 1978.
[4] Bäck, Thomas; Foussette, Christophe; Krause, Peter: Contemporary Evolution Strategies. 1. Aufl.. Berlin Heidelberg: Springer Science & Business Media, 2013.
[5] Rechenberg, I.: Evolutionsstrategie ’94. Stuttgart: Frommann-Holzboog, 1994.
[6] Nissen, V.: Einführung in Evolutionäre Algorithmen: Optimierung nach dem Vorbild der Evolution. 1997. Aufl.. Wiesbaden: Vieweg+Teubner Verlag, 1997.
[7] Kost, B.: Optimierung mit Evolutionsstrategien: eine Einführung in Methodik und Praxis mit Visualisierungsprogrammen. 1. Aufl. Frankfurt am Main: Deutsch, 2003.
[8] Harzheim, Lothar: Strukturoptimierung: Grundlagen und Anwendungen. 2. Aufl. Haan-Gruiten: Europa Lehrmittel Verlag, 2014.
[9] Beyer, Hans-Georg: The Theory of Evolution Strategies. 2001. Aufl.. Berlin Heidelberg: Springer Science & Business Media, 2001.
[10] Schöneburg, Eberhard; Heinzmann, Frank; Feddersen, Sven: Genetische Algorithmen und Evolutionsstrategien: eine Einführung in Theorie und Praxis der simulierten Evolution. Amsterdam: Addison-Wesley, 1994.
